L’intuition tombe à l’eau. Qui reste à bord ? L’IA, car le chaos ne sait jamais quand s’arrêter et l’IA avait déjà prédit la chute.

L’idée même qu’un comportement chaotique puisse être structurant, constructif et utile semble complètement contre-intuitif. Pourtant, en combinant l’intelligence artificielle avec la science des données, les chercheurs découvrent comment le chaos contrôlé (oui ça aussi je vais l’expliquer) peut non seulement résoudre des problèmes complexes mais aussi ouvrir la voie à des innovations révolutionnaires !

Le hasard est un outil scientifique : historiquement, la notion de hasard a été utilisée avec succès dans divers domaines scientifiques. La théorie de Ramsey a été développée pour démontrer l’existence de structures particulières dans des ensembles apparemment chaotiques. La question soulevée dans cette théorie est « combien d’éléments d’une certaine structure doivent être considérés pour qu’une propriété particulière se vérifie ? ». Dans le même esprit, l’ingénieur Claude Shannon (bien connu des gens qui font du traitement du signal) a travaillé sur « l’entropie de Shannon » utilisée pour prouver qu’une communication fiable est possible même sur des canaux bruyants. Ces deux théories exploitent le hasard pour prouver l’existence de solutions où les approches déterministes échouent. Un exemple en image que j’aime tout particulièrement, c’est le papillon de l’attracteur de Lorentz.

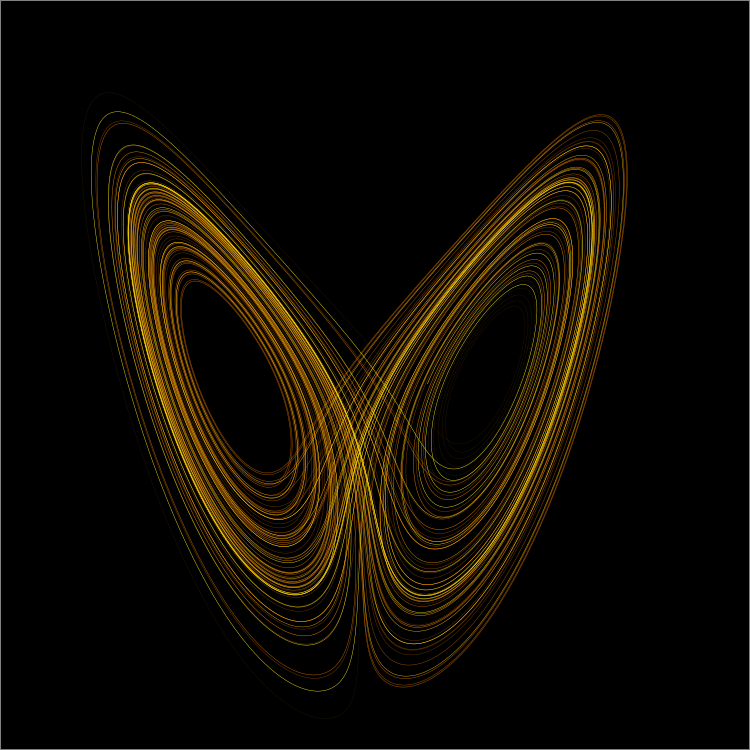
Pour apprécier cette image, il faut déjà la comprendre. Ce papillon, c’est « le résultat d’un système dynamique agissant sur un ensemble de points aléatoires ». C’est l’effet d’un système d’équations réglé dans des conditions très spécifiques, mais qui agit sur les individus (les points) de son environnement indépendamment les uns des autres. Et bien malgré cela, cette forme apparait. En n’observant qu’un point à la fois, il aurait été impossible de déterminer cette structure globale. Mais en regardant un ensemble de points en même temps la nature nous révèle quelques secrets.

Pour visualiser ce qui se passe concrètement, quand on cherche à faire bouger chacun de ces points isolément mais en respectant le même règle de déplacement (source wikipedia):

Bien sûr ce type d’outil parait très théorique, mais en réalité, ça nous permet de comprendre ce qui se passe dans les circuits électriques, en chimie, dans les systèmes stellaires, la convection thermique, la dynamique des fluides, l’acoustique des engrenages, et certainement encore beaucoup de cas que j’ignore. Mais face à une telle structure globale, peut-on encore parler de chaos ? C’est le moment de poser quelques définitions.

La définition du chaos et du hasard : le chaos se réfère à un comportement dynamique d’un système qui est extrêmement sensible aux conditions initiales, une propriété souvent résumée par l’expression “effet papillon”. Dans un système chaotique, de très petites différences dans l’état initial peuvent entraîner des résultats radicalement différents, rendant le comportement du système imprévisible sur le long terme malgré le fait qu’il soit déterministe par nature. En d’autres termes, les systèmes chaotiques sont gouvernés par des lois sous-jacentes, mais leur complexité et leur sensibilité rendent la prédiction exacte pratiquement impossible sur de longues périodes.

Les systèmes chaotiques sont courants en météorologie, en dynamique des populations, en économie, et dans beaucoup d’autres domaines où les interactions complexes et les feedbacks sont présents. Les équations qui les décrivent sont généralement non linéaires, et elles montrent que le chaos est une composante intrinsèque de nombreux systèmes naturels.

Le hasard, décrit des processus ou des événements dont l’issue ne peut pas être prédite avec certitude à partir des informations disponibles avant que l’événement ne se produise. Dans un contexte scientifique, le hasard est souvent modélisé par des probabilités, qui quantifient l’incertitude associée à différents résultats possibles.

En science, le hasard est fondamental en statistique, en théorie des probabilités, et est une composante clé de la mécanique quantique, où il décrit la nature intrinsèquement indéterministe de certains phénomènes physiques à l’échelle atomique et subatomique. Par exemple, le comportement exact d’une particule élémentaire, comme un électron dans un atome, ne peut être décrit que par des fonctions de probabilité, et non par des certitudes absolues (en l’état actuel des connaissances).

On peut donc dire que chaos et hasard sont des concepts vraiment sympas pour décrire l’ordre, la désorganisation, et l’incertitude dans les systèmes scientifiques. Chacun nous permet de mieux comprendre et prévoir le comportement du monde autour de nous.

Et l’IA dans tout ça ? Je ne sais pas ce que je ne sais pas. Par conséquent, chercher à imposer un modèle spécifique aux données pour mieux les modéliser, c’est ignorer les possibilités infinies complémentaires. En introduisant le hasard comme un outil qui nous libère de notre ignorance pour aller chercher un ensemble plus vaste de solutions, on a paradoxalement plus de chance de trouver la bonne solution. Mais pour que ça marche, on se rends vite compte que le temps d’action humaine est un obstacle. C’est pour ça que le hasard, est devenu un puissant allié dans le domaine de l’intelligence artificielle. Le hasard est compatible avec l’IA.

Pour la même raison, détecter des systèmes chaotiques est très complexe pour un physicien parce qu’il a tendance à suivre chaque expérience une à une, alors qu’avec les systèmes d’IA on peut reprendre une vision globale pour détecter des formes non attendues.

Par exemple, dans le domaine de la vision par ordinateur, l’IA utilise le hasard pour optimiser les processus de reconnaissance des formes en introduisant des variations aléatoires dans le processus d’apprentissage, ce qui renforce la robustesse des modèles générés. Paradoxale non ? Les réseaux neuronaux, bénéficient de techniques telles que le “dropout”, où des neurones sont aléatoirement désactivés pendant l’entraînement pour éviter le surajustement et améliorer la généralisation des modèles. Dans le traitement du langage naturel qu’utilisent les LLM, les techniques probabilistes permettent de gérer l’ambiguïté du langage.

La combinaison de ces méthodes nous offre de nouvelles capacités d’analyse et d’observation de ce qui nous entourent, c’est indéniable. C’est aussi un champ de recherche, car bien que cette utilisation ouvre le champ des possibles, il y a aussi des progrès à faire, notamment en termes de prédictivité et de contrôle des résultats.

Ce qu’il faut retenir, c’est que le hasard est là et que c’est un outil d’observation. Penses-tu que tu vas l’utiliser maintenant ?